Previous: Model setting Up: Alternative formulation Next: Conclusion
This is an automatically generated documentation by LaTeX2HTML utility. In case of any issue, please, contact us at info@cfdsupport.com.
Model setting without an explicit use of $ \vec{g}$ in the momentum equation
for the right hand side takes the same values. This is the consequence of a fact that field (![[*]](https://www.cfdsupport.com/wp-content/uploads/2022/02/crossref.png) ) has potential and thus a change in potential energy of an arbitrary element of a fluid is not dependent on its path, but on its initial and final position only.
By introducing
) has potential and thus a change in potential energy of an arbitrary element of a fluid is not dependent on its path, but on its initial and final position only.
By introducing  we formally drop
we formally drop 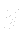 out from the momentum equation. However, in order to obtain the same solution as in the previous settings, it is necessary to alter the presrciption (
out from the momentum equation. However, in order to obtain the same solution as in the previous settings, it is necessary to alter the presrciption (![[*]](https://www.cfdsupport.com/wp-content/uploads/2022/02/crossref.png) ) by adding
) by adding  to its right hand side8.8. By doing this we obtain a new prescription, but this time for the quantity
to its right hand side8.8. By doing this we obtain a new prescription, but this time for the quantity 
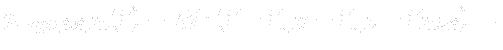
![[*]](https://www.cfdsupport.com/wp-content/uploads/2022/02/crossref.png) ) has potential and thus a change in potential energy of an arbitrary element of a fluid is not dependent on its path, but on its initial and final position only.
By introducing
) has potential and thus a change in potential energy of an arbitrary element of a fluid is not dependent on its path, but on its initial and final position only.
By introducing ![[*]](https://www.cfdsupport.com/wp-content/uploads/2022/02/crossref.png) ) by adding
) by adding 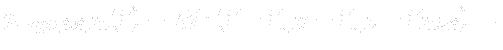
and hence its mean value is zero.
We can see that in this setting there is no need to know a position of a turbine with respect to the water level and there is also no need to even take the measurement of 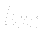 . It only suffice to know
. It only suffice to know 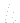 , the head.
, the head.
Previous: Model setting Up: Alternative formulation Next: Conclusion





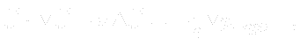
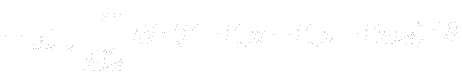
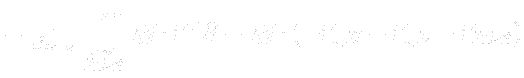
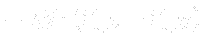
![[*]](https://www.cfdsupport.com/wp-content/uploads/2021/12/crossref.png)