Previous: Center of mass of Up: TCFD- CFD Theory Next: Alternative formulation
This is an automatically generated documentation by LaTeX2HTML utility. In case of any issue, please, contact us at info@cfdsupport.com.
Water turbines - notes on calculations
![[*]](https://www.cfdsupport.com/wp-content/uploads/2022/02/crossref.png) represents a physical setting of a turbine casing with respect to a dam. Let us denote by
represents a physical setting of a turbine casing with respect to a dam. Let us denote by 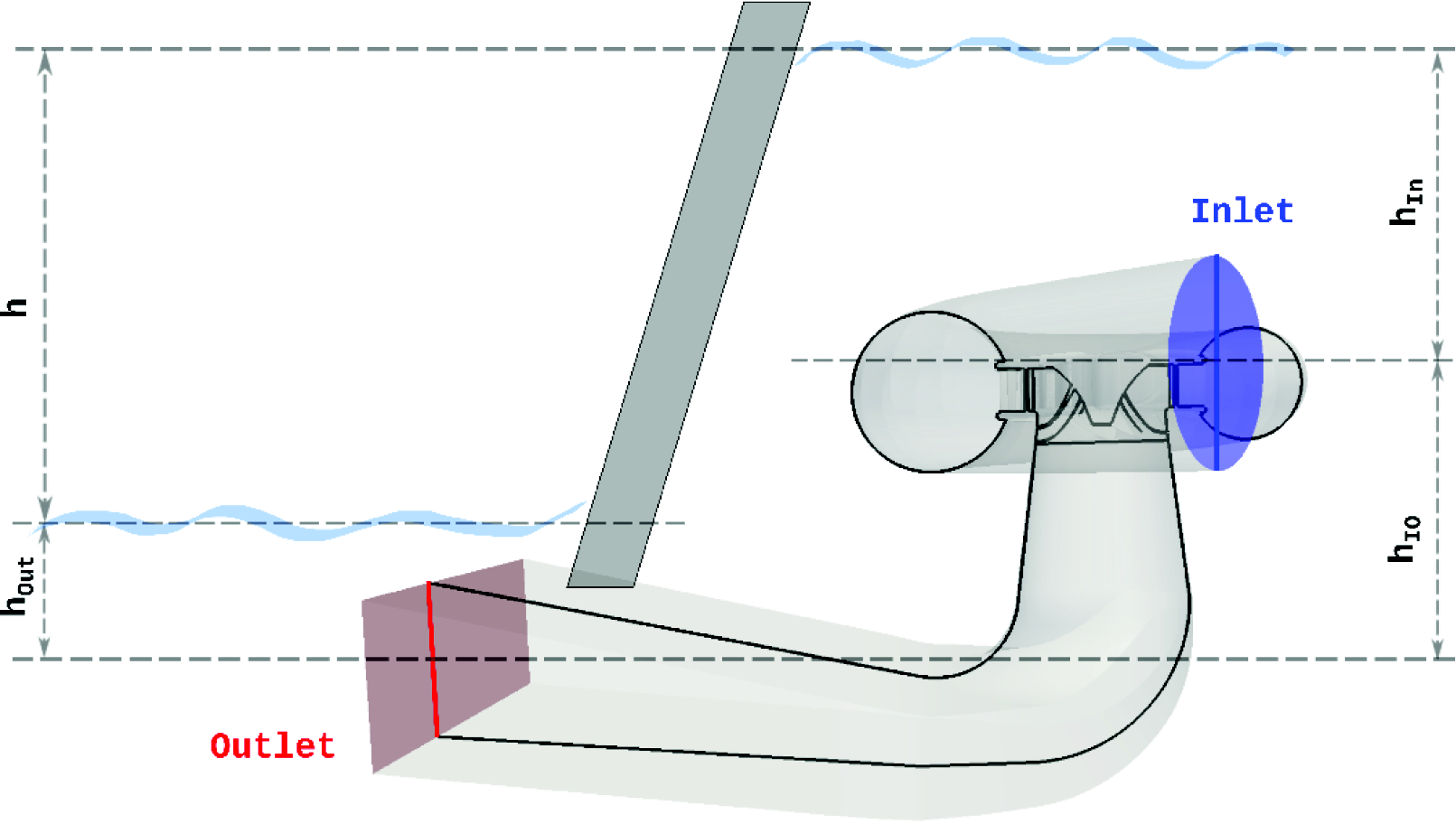
Figure: General water turbine sketch. Physical setting of a turbine casing with respect to a dam. Water levels indicated.
We can see there are several simple relations among quantities just defined
![]()
![]()
![]()
![]()
![]()
![]()
To simplify calculations we usually considers water an incompressible fluid with no phase changes possible and we solve the well known equations, the conservation laws the fluid obeys.
Coservation of linear momentum is expressed by the Navier-Stokes equation. In this case (incompressible fluid, steady state) it can take the form
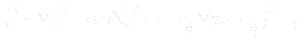
where ![]() is a velocity field,
is a velocity field, ![]() kinematic viscosity,
kinematic viscosity, ![]() density,
density, ![]() pressure field and
pressure field and ![]() is a force density of a gravitational field, given by (
is a force density of a gravitational field, given by (![[*]](https://www.cfdsupport.com/wp-content/uploads/2022/02/crossref.png) ).
).
Conservation of mass is expressed by the continuity equation. In this case it takes the simple form
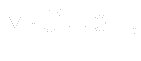
emains to discuss boundary conditions for the equations mentioned above. For we usually do not know the inlet velocity field, we are about to prescribe pressure field for both inlet and outlet surface.
At the inlet surface a total pressure is known and it is equal to hydrostatic one. With the use of formula (![[*]](https://www.cfdsupport.com/wp-content/uploads/2022/02/crossref.png) ) we can write
) we can write
![]()
where ![]() is a position vector of an arbitrary point of the high water level (plane). Since total pressure is defined as a sum of static and dynamical pressure
is a position vector of an arbitrary point of the high water level (plane). Since total pressure is defined as a sum of static and dynamical pressure
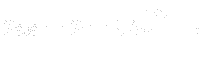
we can, by means of this definition (![[*]](https://www.cfdsupport.com/wp-content/uploads/2022/02/crossref.png) ) and formula (
) and formula (![[*]](https://www.cfdsupport.com/wp-content/uploads/2022/02/crossref.png) ), express
), express ![]() at the inlet
at the inlet
![]()
At the outlet the situation is a little bit complicated. After the flow (with high total pressure) exits the draft tube it mixes with water (with low total pressure) surrounding the draft tube. We usually take simplifying steps and assume the static pressure of exiting flow equals the hydrostatic pressure of surrounding water, i.e. we write
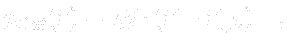
where ![]() is a position vector of an arbitrary point of the low water level.
is a position vector of an arbitrary point of the low water level.
Described steps correspond to real physical setting. In a task like this we need to know not only the ![]() , but even
, but even ![]() (optionally
(optionally ![]() ), i.e. a position of the turbine with respect to the high or low water level. Quantity
), i.e. a position of the turbine with respect to the high or low water level. Quantity ![]() can be obtained from the given turbine casing geometry, of course.
can be obtained from the given turbine casing geometry, of course.
Previous: Center of mass of Up: TCFD- CFD Theory Next: Alternative formulation