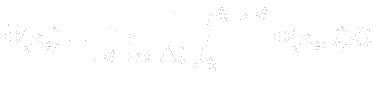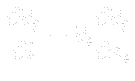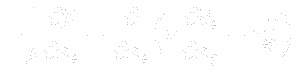Node391 - CFD SUPPORT

Previous: Appendix: RANS Theory Up: Appendix: RANS Theory Next: The closure problem

This is an automatically generated documentation by LaTeX2HTML utility. In case of any issue, please, contact us at info@cfdsupport.com.

Reynolds decomposition (averaging) with respect to time

Statistic approach to turbulence is based on decomposition and time averaging of instantaneous values of variables into mean part and fluctuation part. If the mean value does not depend on choice of initial time (stationary process in mean values) the mean value can be expressed^27.1:

$\displaystyle \bar{\Phi} (x_i) = \lim_{\Delta t \rightarrow \infty} \frac{1}{\Delta t}\int_{t_0}^{t_0 + \Delta t} \Phi (x_i,t) dt$

(27.1)

After Reynolds averaging each instantaneous value can be substitute by its mean part and its fluctuation part:

$\displaystyle a = \bar{a} + a'$

(27.2)

The following rules will be used:

$\displaystyle \bar{a'}$	$\displaystyle =$	0	(27.3)
$\displaystyle \overline{ab}$	$\displaystyle =$	$\displaystyle \overline{a}\overline{b} + \overline{a'b'}$	(27.4)
$\displaystyle \overline{a + b}$	$\displaystyle =$		(27.5)
$\displaystyle \overline{\alpha a}$	$\displaystyle =$	$\displaystyle \alpha \bar{a}$	(27.6)

Here

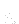and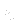

mean the turbulent quantities and $\alpha$ is real constant. Now, let us write the velocity components and pressure in incompressible two dimensional Navier-Stokes equations in the following form:

$\displaystyle u$	$\displaystyle =$	$\displaystyle \bar{u} + u'$	(27.7)
$\displaystyle v$	$\displaystyle =$	$\displaystyle \bar{v} + v'$	(27.8)
$\displaystyle p$	$\displaystyle =$	$\displaystyle \bar{p} + p'$	(27.9)

Substituting these relations in the system of Navier-Stokes equations we obtain the system of Reynolds Averaged Navier-Stokes equations:

$\displaystyle \frac{\partial \bar{v}_i}{\partial x_i}$	$\displaystyle =$	0	(27.10)
$\displaystyle \frac{\partial \bar{v}_j}{\partial t} + \bar{v}_i \frac{\partial \bar{v}_j}{\partial x_i}$	$\displaystyle =$	$\displaystyle - \frac{1}{\rho} \frac{\partial \bar{p}}{\partial x_i} + \frac{\partial}{\partial x_i} \Big( \nu \frac{\partial \bar{v}_i}{\partial x_j} + \tau_{ij}^R \Big)$	(27.11)

where:

$\displaystyle \tau_{ij}^R = - \overline{v'_i v'_j}$

(27.12)

are components of the so-called Reynolds stress tensor. One can see, that this system differs from the original one, just in the term 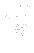$\tau_{ij}^R$ . The tensor 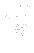$\tau_{ij}^R$ represents six^27.2 (because of symmetry) additional unknowns in our new governing system. Thus, we need to complete the system by some more relations for components of Reynolds stress tensor. This problem is so-called closure problem.

Previous: Appendix: RANS Theory Up: Appendix: RANS Theory Next: The closure problem

OpenFOAM Training by CFD Support, CFD SUPPORT, info@cfdsupport.com +420 212 243 883 © CFD support, s.r.o., Sokolovská 270/201, 190 00 Praha 9, Czech Republic