Previous: Reynolds decomposition (averaging) with Up: Appendix: RANS Theory Next: Algebraic turbulence models
This is an automatically generated documentation by LaTeX2HTML utility. In case of any issue, please, contact us at info@cfdsupport.com.
The closure problem
As it was written, the basic problem of solving RANS is in approximating Reynolds stress tensor. System cannot be closed directly by equations for Reynolds stresses because equations contain unknown correlations of fluctuations of velocity and pressure. For closing the system of equations we have to approximate the Reynolds stress tensor (models of the first order) or approximate unknowns in transport equations for Reynolds stresses (models of the second order).
In 19. century Boussinesq formed hypothesis that exists some analogy between molecular and turbulent viscosity. He claimed that analogically to the Newton’s law, it is possible to express turbulent stress in similar way like shear stress. Using this hypothesis, we can introduce the turbulent eddy viscosity 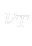 and Reynolds stress tensor can be written in the following way:
This turbulent viscosity hypothesis comes from idea of similarity of molecular transport of momentum with turbulent transport, which is supported by whirls much more greater than are sizes of molecules. Over great differences between these processes Boussinesq hypothesis gives satisfying results.
Introduction of turbulent eddy viscosity does not solve the closure problem. It is only substitution of the Reynolds stress tensor27.3 by turbulent eddy viscosity27.4.
It is necessary to use some turbulence model to evaluate turbulent eddy viscosity. Here we will just mention some basic categorization of RANS models:
and Reynolds stress tensor can be written in the following way:
This turbulent viscosity hypothesis comes from idea of similarity of molecular transport of momentum with turbulent transport, which is supported by whirls much more greater than are sizes of molecules. Over great differences between these processes Boussinesq hypothesis gives satisfying results.
Introduction of turbulent eddy viscosity does not solve the closure problem. It is only substitution of the Reynolds stress tensor27.3 by turbulent eddy viscosity27.4.
It is necessary to use some turbulence model to evaluate turbulent eddy viscosity. Here we will just mention some basic categorization of RANS models:
This work is aimed on algebraic and one-equational models.
 |