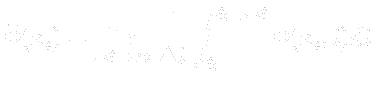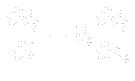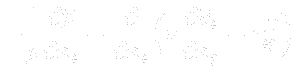Previous: Appendix: RANS Theory Up: Appendix: RANS Theory Next: The closure problem
This is an automatically generated documentation by LaTeX2HTML utility. In case of any issue, please, contact us at info@cfdsupport.com.
Reynolds decomposition (averaging) with respect to time
Statistic approach to turbulence is based on decomposition and time averaging of instantaneous values of variables into mean part and fluctuation part. If the mean value does not depend on choice of initial time (stationary process in mean values) the mean value can be expressed27.1:
After Reynolds averaging each instantaneous value can be substitute by its mean part and its fluctuation part:
The following rules will be used:
Here 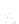 and
and 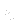 mean the turbulent quantities and
mean the turbulent quantities and  is real constant.
Now, let us write the velocity components and pressure in incompressible two dimensional Navier-Stokes equations in the following form:
Substituting these relations in the system of Navier-Stokes equations we obtain the system of Reynolds Averaged Navier-Stokes equations:
where:
are components of the so-called Reynolds stress tensor. One can see, that this system differs from the original one, just in the term
is real constant.
Now, let us write the velocity components and pressure in incompressible two dimensional Navier-Stokes equations in the following form:
Substituting these relations in the system of Navier-Stokes equations we obtain the system of Reynolds Averaged Navier-Stokes equations:
where:
are components of the so-called Reynolds stress tensor. One can see, that this system differs from the original one, just in the term 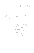 . The tensor
. The tensor 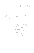 represents six27.2 (because of symmetry) additional unknowns in our new governing system. Thus, we need to complete the system by some more relations for components of Reynolds stress tensor. This problem is so-called closure problem.
represents six27.2 (because of symmetry) additional unknowns in our new governing system. Thus, we need to complete the system by some more relations for components of Reynolds stress tensor. This problem is so-called closure problem.