Node268 - CFD SUPPORT

Defining porosity using Darcy law

Porosity could be modeled using so called Darcy law
The file system/fvOptions defining porous zone named porosity1 should contain following lines (this setup is used for the training case):+

/*--------------------------------*- C++ -*----------------------------------*\
| =========                 |                                                 |
| \\      /  F ield         | OpenFOAM: The Open Source CFD Toolbox           |
|  \\    /   O peration     | Version:  2.3.x                                 |
|   \\  /    A nd           | Web:      www.OpenFOAM.com                      |
|    \\/     M anipulation  |                                                 |
\*---------------------------------------------------------------------------*/
FoamFile
{
    version     2.2;
    format      ascii;
    class       dictionary;
    object      fvOptions;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

porosity1
{
    type          explicitPorositySource;
    active        yes;

    explicitPorositySourceCoeffs
{
    type            DarcyForchheimer;
    selectionMode cellZone;
    cellZone      heatExchanger;

    DarcyForchheimerCoeffs
    {
        d   d [0 -2 0 0 0 0 0] (7.65e7 3e10 3e10);
        f   f [0 -1 0 0 0 0 0] (255 1e5 1e5);

        coordinateSystem
        {
            type    cartesian;  // global co-ordinate system (redundant)
            origin  (0 0 0);    // redundant in this case
            coordinateRotation
            {
                type    axesRotation; // local Cartesian co-ordinates
                e1      (0.998 0.061 0);
                e2      (0.016 -1.000 0);
            }
        }
    }
}

// ************************************************************************* //

Darcy law is based on the resistance characteristics, which is replaced by second order polynomial function, e.g.:

The pressure drop $\mathrm{d}p$ depends on the speed of the fluid.
The parameters d and f can be expressed as

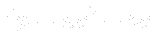
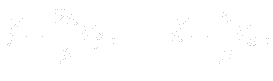
where 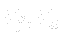are the “flow resistance” vectors in local coordinates of the porous region. In most cases 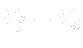. For a flow without friction and confined strictly to the direction, the components would be , i.e. the resistance is zero in the direction and infinite in the other two perpendicular directions 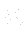and .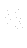
In the example listing above, the flow is weakly confined to the (local) direction, with some friction in this allowed direction and a much greater friction in other two directions.
The local coordinate system is specified by the unit vectors e1 and e2 in the section coordinateSystem. The remaining axis is computed as the cross product e1 e2.
The ith source term component for the momentum equation, provided that user has chosen the canonical basis, reads:

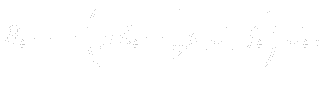
where Einstein notation is not applied