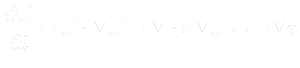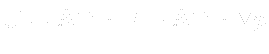Node198 - CFD SUPPORT

Previous: Algorithms PISO and SIMPLE Up: Algorithms PISO and SIMPLE Next: SIMPLE

This is an automatically generated documentation by LaTeX2HTML utility. In case of any issue, please, contact us at info@cfdsupport.com.

PISO

Assume Navier-Stokes equations for incompressible fluid flow
Mass conservation equation (continuity equation)
(11.1)
Momentum conservation equation (velocity equation)
(11.2)
When discretized momentum conservation equation:
(11.3)
Matrix linear system:
(11.4)
Matrix is diagonal, with diagonal of original matrix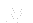
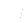is vector corresponding to ()
Rewriting () with substitution from ():
(11.5)
Express 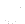from equation (), i.e. momentum correction equation :
(11.6)
We combine momentum correction equation () and continuity equation (), which gives us:
(11.7)
PISO algorithm description:

Computation starts, initial 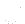and 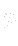are chosen
Time step starts
Boundary conditions are updated
Linear system is solved
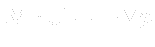
Obtained new
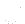
Building matrix and vector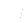
Mass flow over cell faces is computed
Pressure correction is applied ()
Obtained new
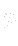
Mass flow over cell faces is corrected
Momentum correction is applied ()
Obtained new corrected
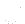
Boundary conditions are updated
Steps 6 – 13 are repeated with respect to nCorrectors value
Time step ends

PISO algorithm in source code:
Take a look at solver icoFoam:
# less $FOAM_SOLVERS/incompressible/icoFoam/icoFoam.C
```
 Info<< "\nStarting time loop\n" << endl;
```

At the beginning of the computation the output is : Starting time loop

    while (runTime.loop())
    {
        Info<< "Time = " << runTime.timeName() << nl << endl;

        #include "readPISOControls.H"
        #include "CourantNo.H"

Cycle over all time steps
Actual time layer is written on the output

Include header files

        fvVectorMatrix UEqn
        (
            fvm::ddt(U)
          + fvm::div(phi, U)
          - fvm::laplacian(nu, U)
        );

Momentum matrix 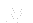is created (UEqn)
UEqn is the left hand side of equation ()
```
        solve(UEqn == -fvc::grad(p));
```

Solves system

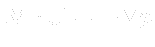
        // --- PISO loop

        for (int corr=0; corr<nCorr; corr++)
        {

Start of PISO algorithm

Loop runs until the repetition reaches the value nCorrectors

            volScalarField rAU(1.0/UEqn.A());

The matrix

is saved as rAU

            volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p));

Evaluates relation

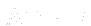and saves to Hbya

           surfaceScalarField phiHbyA
            (
                "phiHbyA",
                fvc::flux(HbyA)
              + fvc::interpolate(rAU)*fvc::ddtCorr(U, phi)
            );

            adjustPhi(phiHbyA, U, p);

            // Update the pressure BCs to ensure flux consistency
            constrainPressure(p, U, phiHbyA, rAU);

            // Non-orthogonal pressure corrector loop
            while (piso.correctNonOrthogonal())
            {
                // Pressure corrector

                fvScalarMatrix pEqn
                (
                    fvm::laplacian(rAU, p) == fvc::div(phiHbyA)
                );

                pEqn.setReference(pRefCell, pRefValue);

                pEqn.solve(mesh.solver(p.select(piso.finalInnerIter())));

Pressure correction loop solves equation

                if (piso.finalNonOrthogonalIter())
                {
                    phi = phiHbyA - pEqn.flux();
                }
            }

Momentum correction

            #include "continuityErrs.H"

Including header file for continuity error evaluation

            U = HbyA - rAU*fvc::grad(p);
            U.correctBoundaryConditions();    
        }

Momentum (velocity) correction
Boundary conditions correction
End of current time step
```
        runTime.write();
```

Writes data to disk (if it is in the time layer where it is told to write down)

        Info<< "ExecutionTime = " << runTime.elapsedCpuTime() << " s"
            << "  ClockTime = " << runTime.elapsedClockTime() << " s"
            << nl << endl;
    }

    Info<< "End\n" << endl;

Writes time information
End of computation

Previous: Algorithms PISO and SIMPLE Up: Algorithms PISO and SIMPLE Next: SIMPLE

OpenFOAM Training by CFD Support, CFD SUPPORT, info@cfdsupport.com +420 212 243 883 © CFD support, s.r.o., Sokolovská 270/201, 190 00 Praha 9, Czech Republic