Previous: Boundary Layer Thickness Up: What is Turbulence? Next: Reynolds number
This is an automatically generated documentation by LaTeX2HTML utility. In case of any issue, please, contact us at info@cfdsupport.com.
Momentum Thickness
The momentum thickness, 
or 
, is the distance by which a surface would have to be moved parallel to itself towards the reference plane in an inviscid fluid stream of velocity 
, or 
to give the same total momentum as exists between the surface and the reference plane in a real fluid.
The definition of the momentum thickness for compressible flow is based on mass flow rate:
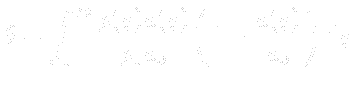
The definition for incompressible flow can be based on volumetric flow rate, as the density is constant:
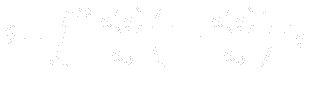
Where 
and 
are the density and velocity in the ‘free stream’ outside the boundary layer, and y is the coordinate normal to the wall.
For boundary layer calculations, the density and velocity at the edge of the boundary layer must be used, as there is no free stream. In the equations above, and are therefore replaced with 
and 
.
For a flat plate at no angle of attack with a laminar boundary layer, the Blasius solution gives
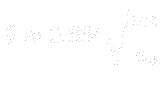
The influence of fluid viscosity creates a wall shear stress, 
, which extracts energy from the mean flow. The boundary layer can be considered to possess a total momentum flux deficit, due to the frictional dissipation.
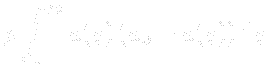
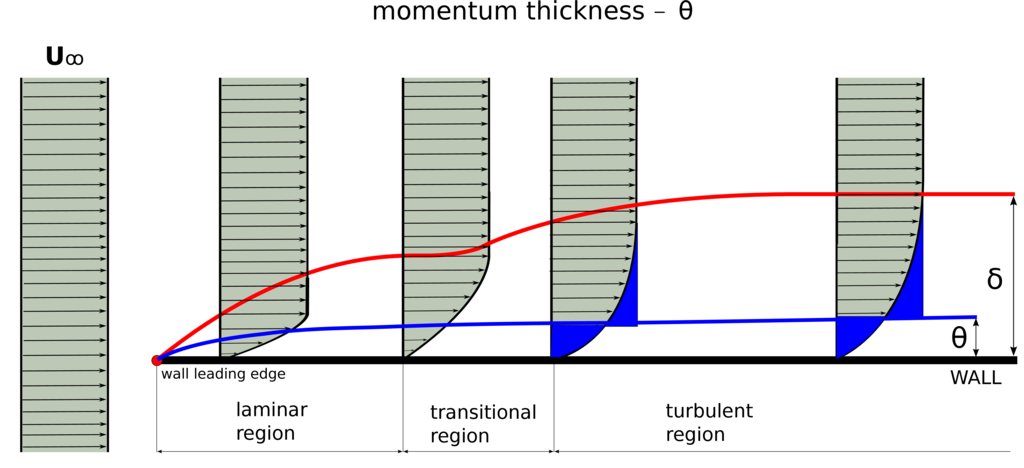
Figure: A simple sketch of boundary layer thickness definition. The sketch also shows the boundary layer development. When the free-stream inlet velocity is uniform and laminar (or low intensity of turbulence). When approaching the wall, the boundary layer is first laminar and then becomes transitional and finally turns to turbulence.