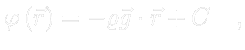1
2
6
5
4
3

Previous: Initial and boundary conditions Up: Computation set-up Next: Initial and boundary conditions

This is an automatically generated documentation by LaTeX2HTML utility. In case of any issue, please, contact us at info@cfdsupport.com.

Turbulent quantities

  • Turbulence parameters are set in file turbulenceProperties in directory constant
  • Print the file on the screen:
    # cat $FOAM_RUN /pitzDaily/constant/turbulenceProperties
    /*--------------------------------*- C++ -*----------------------------------*\
| =========                 |                                                 |
| \\      /  F ield         | OpenFOAM: The Open Source CFD Toolbox           |
|  \\    /   O peration     | Version:  dev                                   |
|   \\  /    A nd           | Web:      www.OpenFOAM.org                      |
|    \\/     M anipulation  |                                                 |
\*---------------------------------------------------------------------------*/
FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    location    "constant";
    object      turbulenceProperties;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

simulationType RAS;

RAS
{
    // Tested with kEpsilon, realizableKE, kOmega, kOmegaSST, v2f,
    // ShihQuadraticKE, LienCubicKE.
    RASModel        kEpsilon;

    turbulence      on;

    printCoeffs     on;
}


// ************************************************************************* //

     

  • Parameter symulationType sets RAS, which stands for Reynolds averaged Navier-Stokes.
  • RAS subdictionary sums up all necessary settings for RAS.
  • RASModel is set to $ k-\epsilon$. Other possibilities are summed up in the commentary.
  • Parameter turbulence can switch turbulence on or off (on/off )
  • Parameter printCoeffs means the turbulence model coefficients are to be printed in standard output to the screen, when solver starts

     

    Selecting RAS turbulence model kEpsilon
RAS
{
    RASModel        kEpsilon;
    turbulence      on;
    printCoeffs     on;
    Cmu             0.09;
    C1              1.44;
    C2              1.92;
    C3              0;
    sigmak          1;
    sigmaEps        1.3;
}
  • Parameter kEpsilonCoeffs is optional, and can change default turbulence model coefficients
  •  

OpenFOAM Training by CFD Support,   CFD SUPPORT,   info@cfdsupport.com    +420 212 243 883      © CFD support, s.r.o., Sokolovská 270/201, 190 00 Praha 9, Czech Republic

6
2
1
5
4
3

Next: Hydrostatic pressure Up: Notes on gravitational potential Previous: Notes on gravitational potential   Contents   Index

Potential of a homogeneous gravitational field

A homogeneous gravitational field is characterized by a constant vector field $ \color{white} \vec{g}$, the well known gravitational acceleration. Let us consider some volume or vessel filled with an incompressible fluid of density $ \color{white} \varrho$. The gravitational field exerts a force on the fluid. Its force density $ \color{white} \vec{f}$ is given by the following well known formula
6 3

It is a simple task to  potential to ([*]). Let us remind, a potential (if it exists) of some given force field $ \color{white} \vec{F}$ is defined as a certain function $ \color{white} \phi$ satisfying the following equation

7 2
We can see that to the $ \color{white} \vec{f}$ given by ([*]) there exists a potential, let us denote it by $ \color{white} \varphi$, stating
8 3
where $ \color{white} C \in \mathbb{R}$ is a constant of integration3.3 and $ \color{white} \vec{r}$ is a position vector3.4.
6
2
1
5
4
3

Next: Hydrostatic pressure Up: Notes on gravitational potential Previous: Notes on gravitational potential   Contents   Index

OpenFOAM Training by CFD Support,   CFD SUPPORT,   info@cfdsupport.com    +420 212 243 883      © CFD support, s.r.o., Sokolovská 270/201, 190 00 Praha 9, Czech Republic
1
2
6
5
4
3

Previous: Virtual Tunnel Efficiency Up: TCFD- CFD Theory Next: blueSolver – steady state,
This is an automatically generated documentation by LaTeX2HTML utility. In case of any issue, please, contact us at info@cfdsupport.com.

TCFD Solvers

Subsections

OpenFOAM Training by CFD Support,   CFD SUPPORT,   info@cfdsupport.com    +420 212 243 883      © CFD support, s.r.o., Sokolovská 270/201, 190 00 Praha 9, Czech Republic