Previous: Prandtl’s mixing length hypothesis Up: Appendix: RANS Theory Next: System of governing equations
This is an automatically generated documentation by LaTeX2HTML utility. In case of any issue, please, contact us at info@cfdsupport.com.
Baldwin - Lomax algebraic model
The Baldwin-Lomax model (Baldwin and Lomax (1978), [10]) is a two-layer algebraic which gives the eddy viscosity 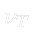 as a function of the local boundary layer velocity profile. The model is suitable for high-speed flows with thin attached boundary-layers, typically present in aerospace and turbomachinery applications. It is commonly used in quick design iterations where robustness is more important than capturing all details of the flow physics. The Baldwin-Lomax model is not suitable for cases with large separated regions and significant curvature/rotation effects.
as a function of the local boundary layer velocity profile. The model is suitable for high-speed flows with thin attached boundary-layers, typically present in aerospace and turbomachinery applications. It is commonly used in quick design iterations where robustness is more important than capturing all details of the flow physics. The Baldwin-Lomax model is not suitable for cases with large separated regions and significant curvature/rotation effects.
where  is the smallest distance from the surface where
is the smallest distance from the surface where 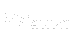 is equal to
is equal to  :
The inner region is given by Prandtl – Van Driest formula:
where:
and
and
The outer region is given by:
where:
where
:
The inner region is given by Prandtl – Van Driest formula:
where:
and
and
The outer region is given by:
where:
where 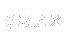 and
and 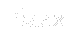 are determined from the maximum of the function:
where
are determined from the maximum of the function:
where 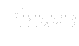 is the intermittency factor given by:
is the intermittency factor given by:
 is the difference between maximum and minimum speed in the profile. For boundary layers the minimum is always set to zero.
The table below gives the model constants present in the formulas above.
is the difference between maximum and minimum speed in the profile. For boundary layers the minimum is always set to zero.
The table below gives the model constants present in the formulas above.
Subsections
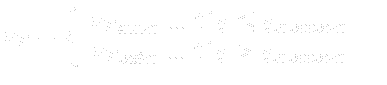 |
(27.17) |
| K | |||||
| 26.0 | 1.6 | 0.3 | 0.25 | 0.41 | 0.0168 |
Subsections





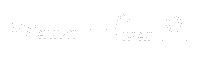
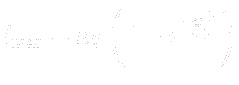
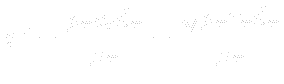
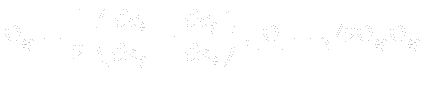
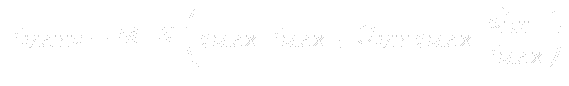
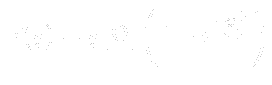
![$\displaystyle F_{KLEB}(y) = \left[1 + 5.5 \left( \frac{y \, C_{KLEB}}{y_{MAX}} \right)^6 \right]^{-1}$](https://www.cfdsupport.com/wp-content/uploads/2022/02/img481.png)